Tutorial Cara Membuat Mahkota Bunga (Flower Crown)

 Pada kesempatan kali ini aku mau berbagi informasi nih tentang cara pembuatan mahkota bunga :)

Ini nih contoh yang udah jadi

  Step 1, kita siapkan bahan-bahannya dulu ya:
-Tang
-Kawat tebal
-Kertas warna hijau untuk menutupi kawat
-Bunga kecil
-Bunga mawar
-Daun kecil
-Kawat kecil, atau kawat tembaga
-Terakhir lem tembak, atau lem lilin.

Ini bahan yang dibutuhkan, siapkan ya!

   Masalah kisaran harga atau berapa banyak biaya yang kita keluarkan itu tidak banyak kok. Aku membeli semua bahan ini kurang lebih Rp.15.000-,. Bahannya juga sangat mudah untuk di dapatkan, kalaian bisa membelinya di toko alat-alat menjahit. Kita berlanjut ke step ke-2 :

Kawat Besar

  Kita simak step yang ini, kawat besar yang tadi sudah disiapkan, kita bentuk sesuai lingkar kepala masing-masing yaa jangan sampai kekecilan apalagi kebesaran haha :p

Kawat, dan kertas hijau untuk batang

    Pada step ini kalian membutuhkan kesabaran. Kawat yang tadinya sudah dibentuk sesuai lingkar kepala, kali ini dililit menggunakan kertas hijau ini, semua harus searah yaa, jangan sampai terputus agar hasilnya lebih rapi. Setelah itu kita lanjut ke step ke 4 :

Bunga, kawat, dan lem

     Ini nih yang paling membutuhkan sebaran. Pada step ini kita mulai menempel bunga pada kawat secara bersilangan yaa. dari merah terus orange begitu seterusnya. Tempelnya menggunakan lem tembak atau lem lilin juga bisa. Tahap terakhir...

Ini tahap terakhir

   Pada tahap terakhir ini kalian tinggal memasang bunga mawar ke sisi yang belum di beri bunga kecil-kecil. FINISH, Sangat muda kan membuatnya, kalian tidak perlu membeli dengan harga yang mahal, cukup membuat sendiri dan tentunya kalian bisa hias sesuka hati kalian. Selamat mencobanya dirumah teman-teman. ;)

Irisan Kerucut ;)

 

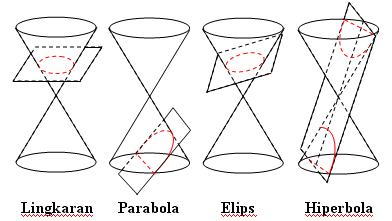
"Terdapat 4 macam irisan kerucut: lingkaran, parabola,elips, hiperbola"

Definisi

Lingkaran
Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu.

• Titik tertentu itu disebut pusat lingkaran
• Jarak yang sama itu disebut jari-jari/radius (r)

Luas lingkaran = π.r² (r = jari-jari)
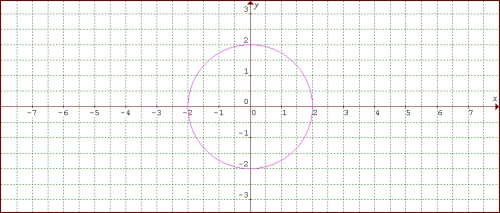
Contoh gambar:
Lingkaran dengan pusat (0, 0) dan jari-jari 2

Parabola
Parabola adalah tempat kedudukan titik-titik yang berjarak sama terhadap sebuah titik dan sebuah garis tertentu.

• Titik itu disebut fokus/titik api (F)
• Garis tertentu itu disebut garis direktris/garis arah
• Garis yang melalui F dan tegak lurus dengan garis arah disebut sumbu simetri parabola
• Titik potong parabola dengan sumbu simetri disebut puncak parabola
• Tali busur terpendek yang melalui F disebut Latus Rectum → tegak lurus dengan sumbu simetri

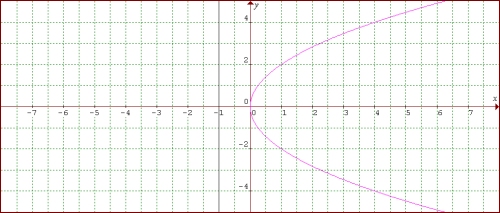
Contoh gambar:
Parabola horisontal dengan puncak (0,0), fokus (1, 0), dan garis arah x = –1

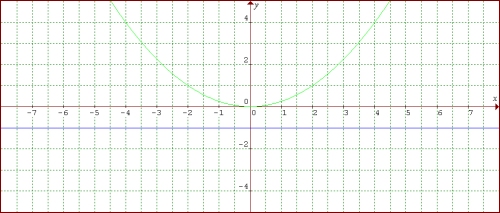
Parabola vertikal dengan puncak (0,0), fokus (0, 1), dan garis arah y = –1

Elips
(1) Elips adalah tempat kedudukan titik-titik yang jumlah jaraknya terhadap 2 titik tertentu tetap.

• Jumlah jarak itu = 2a (untuk elips horisontal) atau 2b (untuk elips vertikal)
• Kedua titik tetap itu disebut fokus (F) → jarak antara F₁ dan F₂ adalah 2c

(2) Elips adalah tempat kedudukan semua titik yang perbandingan jaraknya terhadap sebuah titik dan sebuah garis tetap = e (eksentrisitet), dimana 0 < e < 1

• Titik itu adalah fokus (F), dan garis itu adalah garis arah.
• Ruas garis yang melalui kedua fokus dan memotong elips disebut sumbu mayor
• Pusat elips adalah titik tengah F₁ dan F₂
• Ruas garis yang melalui pusat, tegak lurus sumbu mayor dan memotong elips disebut sumbu minor

Luas Elips = π.a.b  (a = ½ panjang horisontal; b = ½ panjang vertikal)
Contoh gambar:
Elips horisontal dengan pusat (0, 0), puncak-puncak (5, 0), (–5, 0), (0, 4), (0, –4), fokus (3, 0), (–3, 0), dan garis arah x = ±25/3

Elips vertikal dengan pusat (0, 0), puncak-puncak (√2, 0), (–√2, 0), (0, 2), (0, –2), fokus (0,√2), (0, –√2), dan garis arah y = ±2√2/3

Hiperbola
(1) Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap 2 titik tertentu tetap

• Selisih jarak itu = 2a (untuk elips horisontal) atau 2b (untuk elips vertikal)
• Kedua titik tetap itu disebut fokus (F) → jarak antara F₁ dan F₂ adalah 2c

(2) Hiperbola adalah tempat kedudukan semua titik yang perbandingan jaraknya terhadap sebuah titik dan sebuah garis tetap = e , dimana e > 1

• Titik-titik tertentu itu disebut fokus (F₁ dan F₂)
• Garis yang melalui titik-titik F₁ dan F₂ disebut sumbu transvers (sumbu utama)/ sumbu nyata
• Titik tengah F₁ dan F₂ disebut pusat hiperbola (P)
• Garis yang melalui P dan tegak lurus sumbu transvers disebut sumbu konjugasi (sumbu sekawan)/ sumbu imajiner
• Titik-titik potong hiperbola dan sumbu transvers disebut puncak hiperbola
• Garis yang melalui fokus dan tegak lurus pada sumbu nyata dan memotong hiperbola di 2 titik → ruas garis penghubung kedua titik tersebut = Latus Rectum

Contoh gambar:
Hiperbola horisontal dengan pusat (0, 0), puncak (2, 0), (–2, 0), fokus (√6, 0), (–√6, 0),  dan asimtot y = ± ½√2 x

Hiperbola vertikal dengan pusat (0, 0), puncak (√2, 0), (–√2, 0), fokus (0, √6), (0, –√6),  dan asimtot y = ± ½√2 x

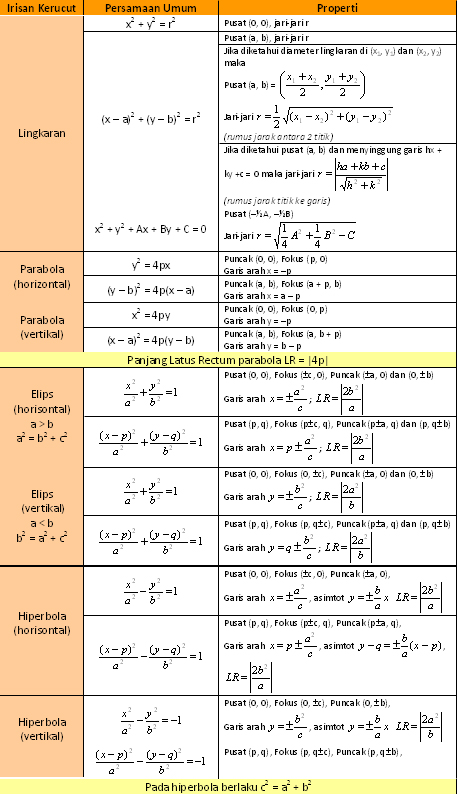
Persamaan

Tips!
Cara membedakan persamaan-persamaan irisan kerucut:

• Pada persamaan Lingkaran: koefisien x² dan y² sama
• Pada persamaan Parabola: hanya salah satu yang bentuknya kuadrat (x² saja atau y² saja)
• Pada persamaan Elips: koefisien x² dan y² bertanda sama (sama-sama positif atau sama-sama negatif)
• Pada persamaan Hiperbola: koefisien x² dan y² berbeda tanda (salah satu positif, yang lain negatif)

Contoh:

• 3x² + 3y² + 6x + y = 5 → Persamaan Lingkaran
• 3x² + 3y + 6x = 5 → Persamaan Parabola
• 3x² + y² + 6x + y = 5 → Persamaan Elips
• 3x² – 3y² + 6x + y = 5 → Persamaan Hiperbola

Kedudukan Titik terhadap Irisan Kerucut

Cara mencari kedudukan titik terhadap kerucut:

1. Jadikan ruas kanan pada persamaan irisan kerucut = 0
2. Masukkan koordinat titik pada persamaan:

→    Jika hasil ruas kiri < 0 → titik berada di dalam irisan kerucut

→    Jika hasil ruas kiri = 0 → titik berada tepat pada irisan kerucut tersebut

→    Jika hasil ruas kanan > 0 → titik berada di luar irisan kerucut

Contoh:
Tentukan kedudukan titik (5, –1) terhadap elips dengan persamaan 3x² + y² + 6x + y = 5
Cara:
3x² + y² + 6x + y – 5 = 0
Ruas kiri: 3.5² + (–1)² + 6.5 + (–1) – 5  = 75 + 1 + 30 – 1 – 5 =100
→ 100 > 0, jadi titik (5, –1) berada di luar elips tersebut

Kedudukan Garis terhadap Irisan Kerucut

Cara mencari kedudukan garis terhadap irisan kerucut:

1. Persamaan garis dijadikan persamaan x = … atau y = …
2. Substitusikan persamaan garis itu pada persamaan irisan kerucut, sehingga menghasilkan suatu persamaan kuadrat.
3. Hitung nilai Diskriminan (D) dari persamaan kuadrat tersebut (Ingat! D = b² – 4.a.c)

→    Jika D < 0 → garis berada di luar irisan kerucut

→    Jika D = 0 → garis menyinggung irisan kerucut di 1 titik

→    Jika D > 0 → garis memotong irisan kerucut di 2 titik

Contoh:
Tentukan kedudukan garis x + 2y = 4 terhadap parabola dengan persamaan 3x² + 3y + 6x = 5
Cara:
Garis: x = 4 – 2y
3(4 – 2y)² + 3y + 6(4 – 2y) – 5 = 0
3(16 – 16y + 4y²) + 3y + 24 – 12y – 5 = 0
48 – 48y + 12y² + 3y + 24 – 12y – 5 = 0
12y² – 57y + 67 = 0
D = b² – 4.a.c = (–57)² – 4.12.67 = 33
Karena D > 0 maka garis x + 2y = 4 memotong parabola tersebut

Persamaan Garis Singgung

Persamaan garis singgung dengan gradien m

Persamaan garis singgung pada titik (x₁, y₁)
→ selalu gunakan sistem bagi adil:

(…)² menjadi (…).(…)

(…) menjadi ½ (…) + ½ (…)

Pada salah satu (…) akan dimasukkan koordinat titik yang diketahui

→ masukkan titik ke persamaan hasil bagi adil

1. Jika titik terletak pada irisan kerucut, akan menghasilkan persamaan garis singgung
2. Jika titik terletak di luar irisan kerucut, akan menghasilkan persamaan garis polar

Potongkan garis polar dengan irisan kerucut untuk mendapatkan 2 titik potong
Masukkan kedua titik potong itu ke dalam persamaan hasil bagi adil untuk mendapatkan 2 buah persamaan garis singgung

Contoh 1:
Tentukan persamaan garis singgung pada lingkaran x² + y² + 4x = 13 pada titik (2, 1)
Cara:
(2, 1) terletak pada lingkaran (2² + 1² + 4.2 = 13)
Persamaan bagi adil:
x₁.x + y₁.y + 2.x₁ + 2.x = 9
Masukkan (2, 1) sebagai x₁ dan y₁:
2.x + 1.y + 2.2 + 2.x = 9
4x + y – 5 = 0 → persamaan garis singgung

Contoh 2:
Tentukan persamaan garis singgung pada lingkaran x² + y² + 4x = 13 pada titik (4, 1)
Cara:
(4, 1) terletak di luar lingkaran (4² + 1² + 4.4 = 33 > 16)
Persamaan bagi adil:
x₁.x + y₁.y + 2.x₁ + 2.x = 9
Masukkan (4, 1) sebagai x₁ dan y₁:
4.x + 1.y + 2.4 + 2.x = 9
6x + y – 1 = 0 → persamaan garis polar
y = 1 – 6x
Substitusikan persamaan garis polar ke dalam persamaan lingkaran:
x² + (1 – 6x)² + 4x – 13 = 0
x² + 1 – 12x + 36x² + 4x – 13 = 0
37x² – 8x – 12 = 0
Gunakan rumus abc:

Masukkan (x₁, y₁) dan (x₂, y₂) ke dalam persamaan hasil bagi adil

Jenis dan Macam Pengangguran :)

Jenis dan Macam Pengangguran

Berdasarkan Jam Kerja

Berdasarkan jam kerja, pengangguran dikelompokkan menjadi 3 macam:

• Pengangguran Terselubung (Disguised Unemployment) adalah tenaga kerja yang tidak bekerja secara optimal karena suatu alasan tertentu.
• Setengah Menganggur (Under Unemployment) adalah tenaga kerja yang tidak bekerja secara optimal karena tidak ada lapangan pekerjaan, biasanya tenaga kerja setengah menganggur ini merupakan tenaga kerja yang bekerja kurang dari 35 jam selama seminggu.
• Pengangguran Terbuka (Open Unemployment) adalah tenaga kerja yang sungguh-sungguh tidak mempunyai pekerjaan. Pengganguran jenis ini cukup banyak karena memang belum mendapat pekerjaan padahal telah berusaha secara maksimal.

Berdasarkan penyebab terjadinya

Berdasarkan penyebab terjadinya, pengangguran dikelompokkan menjadi 9 macam:

• Pengangguran friksional (frictional unemployment)

Pengangguran friksional adalah pengangguran karena pekerja menunggu pekerjaan yang lebih baik.

• Pengangguran Struktural (Structural unemployment)

Pengangguran yang disebabkan oleh penganggur yang mencari lapangan pekerjaan tidak mampu memenuhi persyaratan yang ditentukan pembuka lapangan kerja.

• Pengangguran Teknologi (Technology unemployment)

Pengangguran yang disebabkan perkembangan/pergantian teknologi. Perubahan ini dapat menyebabkan pekerja harus diganti untuk bisa menggunakan teknologi yang diterapkan.

• Pengangguran Siknikal

Pengangguran yang disebabkan kemunduran ekonomi yang menyebabkan perusahaan tidak mampu menampung semua pekerja yang ada. Contoh penyebabnya, karena adanya perusahaan lain sejenis yang beroperasi atau daya beli produk oleh masyarakat menurun.

• Pengangguran Musiman

Pengangguran akibat siklus ekonomi yang berfluktuasi karena pergantian musim. Umumnya pada bidang pertanian , perikanan. Contoh lainnya, para petani.

• Setengah Menganggur

Pengangguran dimana pekerja yang hanya bekerja dibawah jam normal (sekitar 7-8 jam per hari)

• Pengangguran Keahlian/Pengangguran Tidak Kentara
• Pengangguran Keahlian adalah disebabkan karena tidak adanya lapangan kerja yang sesuai dengan bidang keahlian. Pengangguran tidak kentara adalah punya aktifitas berdasarkan keahliannya tetapi tidak menerima uang. Contoh untuk point ini adalah anak sekolah (siswa) atau mahasiswa. Mereka adalah ahli pencari ilmu, tetapi mereka tidak menghasilkan uang dan justru harus mengeluarkan uang atau biaya, misalnya harus membeli paket buku LKS atau membayar biaya kursus yang diselenggarakan oleh sekolahnya sendiri. Contoh lainnya adalah (misalnya) seorang pelatih pencak silat yang tidak meminta gaji dari organisasinya. Pengangguran tidak kentara ini, juga bisa disebut sebagai Pengangguran Terselubung.
• Pengangguran Total adalah benar-benar tidak mendapat pekerjaan, karena tidak adanya lapangan kerja atau tidak adanya peluang untuk menciptakan lapangan kerja.
• Pengangguran Unik. Pengangguran jenis ini adalah pekerja yang menerima gaji secara rutin tanpa pemotongan, tetapi ditempat kerjanya hanya sering diisi dengan bercerita sesama pekerja karena minimnya pekerjaan yang harus dikerjakan. Hal ini disebabkan karena tempat kerjanya kelebihan tenaga. Perkecualian, semisal pegawai atau petugas Pemadam Kebakaran atau Penanggulangan Bencana Alam. Pegawai atau petugas semisal ini tenaganya harus disimpan dan dipersiapkan secara khusus jika ada pelatihan atau simulasi atau harus diterjunkan pada situasi sebenarnya.

Penyebab Pengangguran

Pengangguran umumnya disebabkan karena jumlah angkatan kerja tidak sebanding dengan jumlah lapangan pekerjaan yang mampu menyerapnya. Pengangguran seringkali menjadi masalah dalam perekonomian karena dengan adanya pengangguran, produktivitas dan pendapatan masyarakat akan berkurang sehingga dapat menyebabkan timbulnya kemiskinan dan masalah-masalah sosial lainnya.
Tingkat pengangguran dapat dihitung dengan membandingkan jumlah pengangguran dengan jumlah angkatan kerja yang dinyatakan dalam persen.
Ketiadaan pendapatan menyebabkan penganggur harus mengurangi pengeluaran konsumsinya yang menyebabkan menurunnya tingkat kemakmuran dan kesejahteraan. Pengangguran yang berkepanjangan juga dapat menimbulkan efek psikologis yang buruk terhadap penganggur dan keluarganya.
Tingkat pengangguran yang terlalu tinggi juga dapat menyebabkan kekacauan politik, keamanan dan sosial sehingga mengganggu proses pembangunan.

Akibat pengangguran

Bagi Perekonomian Negara

1. Penurunan pendapatan perkapita.
2. Penurunan pendapatan pemerintah yang berasal dari sektor pajak.
3. Meningkatnya biaya sosial yang harus dikeluarkan oleh pemerintah.
4. Dapat menambah hutang negara.

Bagi Masyarakat

1. Pengangguran merupakan beban psikologis dan psikis.
2. Pengangguran dapat menghilangkan keterampilan, karena tidak digunakan apabila tidak bekerja.
3. Pengangguran akan menimbulkan ketidakstabilan sosial dan politik.

PENGGOLONGAN TENAGA KERJA

 Penggolongan tenaga kerja :

 1 .Berdasarkan kemampuan.
a.Tenaga kerja terdidik/ tenaga ahli/tenaga mahir
Tenaga kerja terdidik adalah tenaga kerja yang mendapatkan suatu keahlian atau kemahiran padasuatu bidang karena sekolah atau pendidikan formal dan non formal. Contohnya seperti sarjanaekonomi, insinyur, sarjana muda, doktor, master, dan lain sebagainya.

b.Tenaga kerja terlatih.
Tenaga kerja terlatih adalah tenaga kerja yang memiliki keahlian dalam bidang tertentu yangdidapat melalui pengalaman kerja. Keahlian terlatih ini tidak memerlukan pendidikan karenayang dibutuhkan adalah latihan dan melakukannya berulang-ulang sampai bisa dan menguasai pekerjaan tersebut.
Contohnya adalah supir, pelayan toko, tukang masak, montir, pelukis, danlain-lain.

c.Tenaga kerja tidak terdidik dan tidak terlatih.Tenaga kerja tidak terdidik dan tidak terlatih adalah tenaga kerja kasar yang hanyamengandalkan tenaga saja. Contoh tenaga kerja model ini seperti kuli, buruh angkut, buruh pabrik, pembantu, tukang becak, dan masih banyak lagi contoh lainnya.

2.Penggolongan tenaga kerja menurut sifatnya dibedakan menjadi:
a.Tenaga keja jasmani yaitu tenaga kerja yang mengandalkan fisik atau jasmani dalam proses produksi
b.Tenaga kerja rohani yaitu tenaga kerja yang memerlukanpikiran untuk melakukan dalam proses produksi

3.Penggolongan tenaga kerja menurut fungsi pokok dalam perusahaan.
a.Tenaga kerja bagian produksi.
b.Tenaga kerja bagian pemasaran.
c.Tenaga kerja bagian umum dan administrasi

.4.Penggolongan tenaga kerja menurut hubungan dengan produk
a.Tenaga kerja langsung
b.Tenaga kerja tidak langsung

5.Penggolongan tenaga kerja menurut kegiatan departemen-departemen dalam perusahaan.
a.Tenaga kerja departemen produksi
b.Tenaga kerja departemen non produksi

6.Penggolongan tenaga kerja menurut jenis pekerjaannya.
a.Tenaga kerja bagian pabrik
b.Tenaga kerja bagian kantor
c.Tenaga kerja bagian lapangan